Разработан новый алгоритм для измерения энтропии запутанности

Эта ключевая исследовательская работа недавно была опубликована в одном из самых престижных журналов по физике – Физические обзорные письма.

Квантовые материалы играют жизненно важную роль в продвижении человека. Поиск более новых квантовых материалов с исключительными свойствами был насущным среди научного и технологического сообщества.

2D-муаровые материалы, такие как витой двухслойный графен, играют далеко идущую роль в исследовании новых квантовых состояний, таких как сверхпроводимость, которая не страдает электронным сопротивлением. Они также играют определенную роль в развитии «квантовых компьютеров», которые значительно превосходят лучшие существующие суперкомпьютеры.

Но материалы могут прийти только в «квантовое состояние», то есть когда тепловые эффекты больше не могут препятствовать квантовым флуктуациям, которые вызывают квантовые фазовые переходы между различными квантовыми состояниями или квантовыми фазами, при чрезвычайно низких температурах (около абсолютного нуля, -273,15 ° C) или при исключительно высоком давлении. Поэтому эксперименты, проверяющие, когда и как атомы и субатомные частицы различных веществ «свободно общаются и взаимодействуют друг с другом через запутанность» в квантовом состоянии, непомерно дороги и сложны в выполнении.

Исследование еще более осложняется неспособностью классической структуры LGW (Landau, Ginzburg, Wilson) описать определенные квантовые фазовые переходы, получившие название Deconfined Quantum Critical Points (DQCP). Тогда возникает вопрос, можно ли найти реалистичные модели решетки DQCP для устранения несоответствий между DQCP и QCP. Целенаправленное исследование темы приводит к обильным численным и теоретическим работам с противоречивыми результатами, а решение остается неуловимым.

Г-н Цзяруй ЧЖАО, д-р Чжэн Янь и д-р Цзы Ян МЭН из Департамента физики, HKU успешно сделали важный шаг к решению проблемы путем изучения квантовой запутанности, которая отмечает фундаментальное различие между квантовой и классической физикой.

Исследовательская группа разработала новый и более эффективный квантовый алгоритм методов Монте-Карло, принятых учеными для измерения энтропии запутанности объектов Реньи. С помощью этого нового инструмента они измерили энтропию запутанности Реньи в DQCP и обнаружили, что масштабирующее поведение энтропии, то есть то, как энтропия изменяется с размерами системы, резко контрастирует с описанием обычных типов фазовых переходов LGW.

«Наши результаты помогли подтвердить революционное понимание теории фазового перехода, отрицая возможность сингулярной теории, описывающей DQCP. Вопросы, поднятые нашей работой, будут способствовать дальнейшим прорывам в поиске всестороннего понимания неизведанной территории», – сказал д-р Чжэн Ян.

«Это открытие изменило наше понимание традиционной теории фазового перехода и поднимает много интригующих вопросов о деконтинированной квантовой критичности. Мы надеемся, что этот новый инструмент, разработанный нами, поможет процессу разблокировки загадки квантовых фазовых переходов, которая озадачивала научное сообщество в течение двух десятилетий», — сказал г-н Чжао Цзяруй, первый автор журнальной статьи и аспирант, который придумал окончательные исправления алгоритма.

«Это открытие приведет к более общей характеристике критического поведения новых квантовых материалов и является шагом ближе к актуализации применения квантовых материалов, которые играют жизненно важную роль в продвижении человека». Д-р Мэн Цзы Ян заметил.

Модели
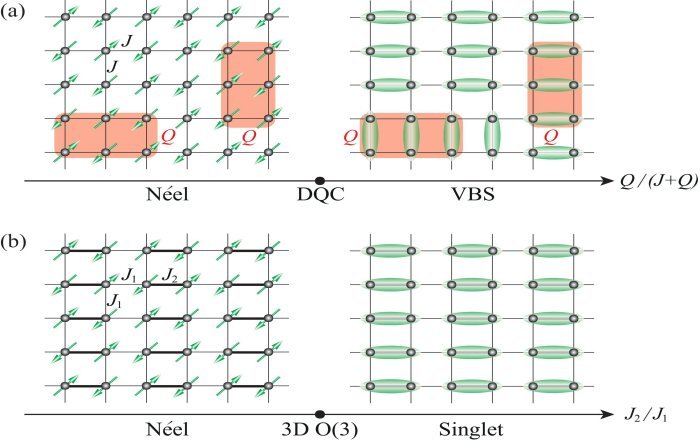
Чтобы проверить эффективность и превосходную мощность алгоритма и продемонстрировать четкую разницу между энтропией запутанности нормального QCP между DQCP, исследовательская группа выбрала две репрезентативные модели — J.₁-Дж₂ модель, в которой размещаются обычные O(3) QCP и J-Q₃ модель размещения DQCP, как показано в Изображение 2.

Алгоритм приращения неравновесия
Основываясь на предыдущих методах, исследовательская группа создала высокопараллельный алгоритм приращения. Как показано в Изображение 3, основная идея алгоритма заключается в разделении всей задачи моделирования на множество более мелких задач и использовании массивных процессоров для параллельного выполнения меньших задач, что значительно сокращает время моделирования. Этот улучшенный метод помог команде смоделировать две модели, упомянутые ранее, с высокой эффективностью и лучшим качеством данных.

Выводы
С помощью метода неравновесного приращения исследовательская группа успешно получила вторую энтропию запутанности Реньи S_A⁽²⁾ в QCP и DQCP двух моделей для разных размеров системы. Данные показаны в Изображение 4, и из отступлений можно обнаружить, что при вычитании ведущего термина (вклад закона области из границы запутанности) признаки подведомственного термина четко различают QCP (отрицательный в J₁-Дж₂ model,) и DQCP (положительный в J-Q₃ модель). Это открытие исключает возможность описания DQCP на основе унитарного предположения и поднимает несколько интригующих вопросов о теории DQC. Это открытие, вероятно, приведет к более общей характеристике критического поведения новых квантовых материалов.