Использование атомных возбуждений для измерения вращения пространства-времени

Как поведут себя атомы вблизи сверхмассивного объекта? Мы знаем, как ведут себя атомы в условиях крайне слабой гравитации, подобной той, что существует у поверхности Земли: Они могут переходить с более низкого энергетического уровня на более высокий, когда электрон поглощает фотон или ядро поглощает гамма-лучи, и так далее. Но что если атом находится в сильном гравитационном поле, например, вблизи сверхмассивной, вращающейся черной дыры или вращающейся нейтронной звезды?

Двое ученых из Пекинского исследовательского центра вычислительной техники в Китае установили, что количество возбуждения также будет зависеть от того, насколько быстро вращается пространство-время за пределами массивного объекта. По их словам, обратная картина может оказаться полезной: Измерение изменений в наборе возбуждений может быть использовано для определения скорости вращения пространства-времени — явление, называемое «перетягиванием рамки».

Результаты исследования опубликованы на сервере препринтов arXiv.

Затягивание кадров — это предсказание теории гравитации Эйнштейна, называемой общей относительностью. Подобно тому как неподвижная черная дыра деформирует пространство вокруг себя, что приводит к появлению горизонта событий и кажущейся сингулярности в ее центре, в 1918 году австрийские физики Йозеф Ленсе и Ганс Тирринг обнаружили, что вращение массивного объекта будет тянуть пространство вокруг него в направлении вращения.

Таким образом, измерения расстояний и углов вблизи массы изменяются, а пространство и время могут даже частично смешиваться относительно наблюдателя, находящегося на большом расстоянии.

Известный как эффект Ленса-Тирринга, он существует даже в пределе «слабого поля» уравнений Эйнштейна, как пространство вблизи горизонта событий черной дыры, где гравитация не слишком сильна (но сильнее, чем на Земле).

НАСА и другие группы нашли астрономические свидетельства перетягивания кадров, хотя исследователи говорят, что измерения должны быть более точными. Скорость вращения при перетаскивании зависит от углового момента массы (насколько быстро она вращается) и массы, а также от расстояния до нее.

В этом исследовании ученые предположили, что небольшая масса (например, атом или другой объект с энергетическими уровнями) окружена простым квантовым полем, которое существует везде за пределами центральной вращающейся массы.

Связанные с квантовым полем частицы имеют нулевой спин (в квантово-механическом смысле); одним из примеров может быть электромагнитное поле, где носители силы поля, фотоны, имеют нулевой спин. Отразится ли угловая частота перетаскивания рамки на скорости возбуждения атома?

В более простом случае невращающейся черной дыры, так называемом «решении Шварцшильда» для уравнений Эйнштейна, никакого перетягивания рамки нет. Известно, что атом, находящийся в состоянии покоя, будет возбужден излучением Хокинга черной дыры — излучением со спектром частот черного тела, которое испускается на горизонте событий, окружающем черную дыру. Скорость возбуждения атома содержит информацию о силе гравитационного поля на горизонте событий.

Однако для вращающейся массивной черной дыры, которая имеет так называемое «решение Керра» (которое было найдено только в 1963 году), не существует истинных горизонтов событий и сингулярностей. В пространственном времени Керра действительно наблюдается перетягивание рамки, но атом, находящийся в состоянии покоя, не возбуждается.

В отличие от решения Шварцшильда, решение Керра является точным решением для структуры пространства-времени даже для очень больших масс и сильной гравитации. Поэтому соавторы работы Руй-Чен Лю и К. П. Сун рассмотрели случай атома, движущегося по кругу с постоянной скоростью в пространстве-времени Керра.

Они «квантовали» поле с нулевым спином, то есть рассматривали его в соответствии с правилами квантовой механики (которые отличаются от знаменитых уравнений Максвелла, рассматривающих электромагнитные поля как классические, без фотонов или частиц с нулевым спином). Сложив все это вместе и проработав математику, они пришли к выводу, что атом будет возбужден.

Далее они обнаружили, что скорость возбуждения — количество возбуждений в секунду — такая же, как у атома, погруженного в тепловую ванну (окруженного энергией) при температуре, пропорциональной ускорению атома при движении по кругу. Это напоминает эффект Унруха, когда атом, испытывающий постоянное ускорение в пустом вакууме, даже двигаясь по прямой линии, видит частицы и тепловую ванну с чрезвычайно малой, но ненулевой температурой.

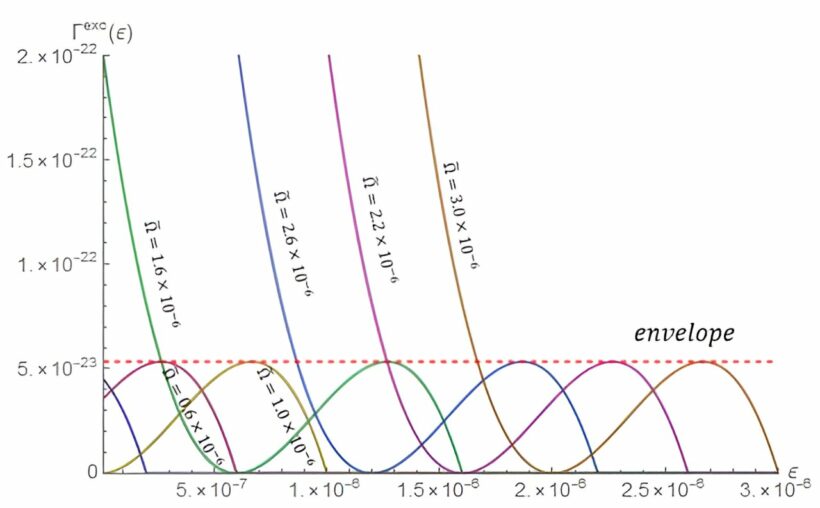
Для дальнейшего анализа Лю и Сон рассмотрели различные энергии возбуждения для атомов, вращающихся с разными скоростями и на разных расстояниях от центральной массы, и обнаружили, что скорости возбуждения оказываются между 0 и верхней границей для всех значений вращательной частоты перетаскивания рамки.

Они пишут: «Эффект перетягивания рамки генерирует отдельную скорость возбуждения для атомов, находящихся в круговом движении». Эту верхнюю границу можно измерить, а по ней и по радиусу движения можно определить скорость вращения, вызванную эффектом перетягивания рамки.

Авторы отмечают, что их подход использует нелокальные свойства квантовых полей, также известные как запутанность, с помощью измерений, которые не зависят от традиционной звездной калибровки, в которой используются звезды с известными световыми характеристиками для определения качества и надежности датчиков телескопа.